The Tangent SNL - Exploring Unexpected Shifts

08 Jul, 2025

Have you ever been watching something, perhaps a comedy sketch or a lively discussion, when suddenly, the whole thing takes a surprising turn? It’s almost like the conversation or the storyline just brushes up against a new idea, then veers off in a completely different direction. That feeling, that moment of an abrupt change in course, actually has a rather interesting parallel in the world of shapes and measurements. You know, that sudden shift, it’s a lot like something we call a "tangent."

You see, the word "tangent" isn't just about sharp changes in a chat. It also describes a very specific concept in geometry, and it pops up quite a bit in the study of angles and triangles. It’s a way of looking at how lines meet curves or how sides of a triangle relate to each other. So, in some respects, it’s about connections, but also about how things can move away from those connections.

We’re going to take a closer look at this idea, peeling back the layers to see what it really means, from lines that just kiss a circle to the way we measure parts of a triangle. It’s a concept that, honestly, is pretty fundamental to how we think about shapes and spaces. We’ll even consider how this mathematical idea might, just might, echo those sudden, funny shifts you see in comedy, or, well, anywhere really.

What's the Big Deal with the Tangent Line?
- Just a Touch - The Tangent SNL's Geometric Side
So, How Does a Triangle Get Tangent-ed?
- Ratios and Right Angles - The Tangent SNL's Mathematical Heart
Is There More to the Tangent Story?
- A Sudden Turn - The Tangent SNL as a Shift
Where Do We Even Use the Tangent?
- Figuring Things Out - The Tangent SNL in Action

What's the Big Deal with the Tangent Line?

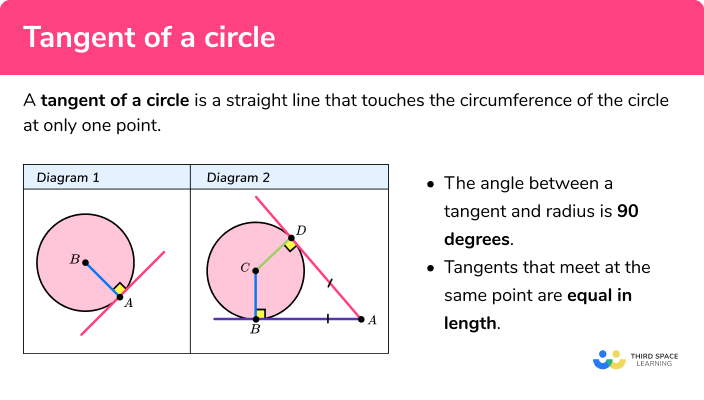
Think about a line that just barely touches a curve. It doesn't cut through it, and it doesn't cross over to the other side. It simply makes contact at one single spot. This is, you know, what we often picture when we talk about a tangent line in geometry. It's like a fleeting handshake between a straight path and a curvy one, just a brief connection before they go their separate ways. This line also kind of matches the curve's lean or tilt at that specific point. It gives us a sense of the curve's immediate direction.

Just a Touch - The Tangent SNL's Geometric Side

So, when we consider a flat shape, a line that just makes contact with its edge at one point is, in essence, what we call a tangent. It’s a straight line that, you know, doesn't actually go inside the curve or shape. It only grazes the outside, exactly where it meets the curve. This idea is really quite important for understanding how shapes behave, especially when you think about how they change direction or how steep they might be at any given spot. It’s a foundational idea, really, for lots of other mathematical concepts.

Picture a wheel rolling along the ground. The ground itself is a tangent line to the wheel at the point where they meet. The wheel is constantly, you know, creating new tangent points as it moves. This simple image helps us grasp that a tangent isn't just some abstract idea. It's something we see all the time, even if we don't always call it by its proper name. It shows us the exact direction the wheel is moving at that very instant. It’s a very precise sort of connection, you know, a very specific kind of touch.

The straight line that just touches a curve at one particular spot is also said to be matching the curve's slope right there. This means it has the exact same steepness or flatness as the curve at that single point of contact. It's almost like the line is mimicking the curve's immediate inclination. This concept is pretty central to, well, lots of things in mathematics, especially when you start looking at how things change over time or space. It gives us a way to measure the instant lean of a curved path, which is, you know, quite helpful.

This geometric idea of a tangent line is pretty useful. It helps us figure out things like the direction a moving object is going at a specific moment, or how quickly something is changing. It's like, you know, getting a snapshot of a curve's behavior at a single, isolated point. So, while it might sound a bit academic, it actually has a lot of practical uses when you think about it. It’s really about understanding how things interact, even if it’s just a line and a curve meeting for a moment.

So, How Does a Triangle Get Tangent-ed?

Now, let's switch gears a bit and talk about triangles. Specifically, right-angled triangles. These are the ones with, you know, one corner that makes a perfect square shape, like the corner of a book. In these triangles, we have something called "sine," "cosine," and "tangent." These are, basically, ways to compare the lengths of the sides of the triangle using ratios. A ratio is just, you know, dividing one length by another. It tells you how many times one side fits into another.

Ratios and Right Angles - The Tangent SNL's Mathematical Heart

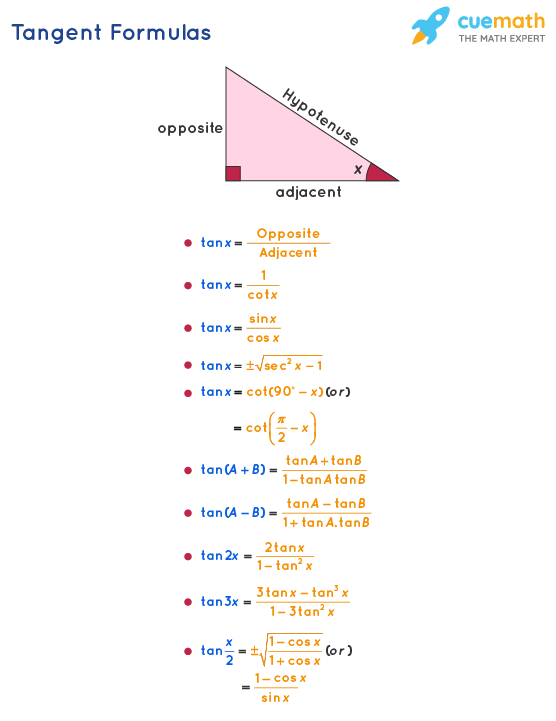
For a right-angled triangle, when you pick one of the angles that isn't the square one, let's call it theta, the tangent value for that angle is, you know, a specific comparison. It’s found by taking the length of the side that is directly across from that angle and dividing it by the length of the side that is right next to it, but not the longest side. This is, in fact, a fundamental part of trigonometry, which is a branch of mathematics that deals with triangles and angles. It’s one of the main ways we describe the relationships between parts of a triangle.

So, you take the side that’s opposite your chosen angle, and you, you know, put its length over the side that’s adjacent to it. That’s the tangent ratio. It’s written as "tan" followed by the angle, like "tan x." This particular comparison is one of the six main functions in trigonometry. These functions help us, you know, figure out missing pieces of information in triangles, like how long a side is or how big an angle is, just by knowing a few other bits. It’s a pretty clever system, if you ask me, and quite useful for building things or, you know, mapping out spaces.

In a right triangle, the tangent of an angle is, therefore, the ratio of the length of the side that faces the angle to the length of the side that sits beside the angle. It’s like saying, "How many times does the side next to it fit into the side across from it?" This ratio is also, in other words, the result of dividing the sine of that angle by its cosine. So, it's connected to other important trigonometric ideas, too. It’s a very specific way to describe the steepness or flatness of an angle within the triangle, you know, based on its sides.

To really get a handle on these functions, it helps to, you know, give names to each side of the triangle. There’s the side opposite the angle you’re looking at, the side adjacent to it (which means next to it), and then there’s the longest side, called the hypotenuse. The tangent specifically focuses on the opposite and adjacent sides. These tangent formulas, as they are called, are, well, just ways to express these relationships. They help us understand how angles and side lengths are tied together in a right triangle, which is, you know, pretty cool.

For any right triangle with an angle we call alpha (α), the tangent of alpha, or tan(α), is, you know, defined as the comparison between the side that is across from angle α and the side that is right next to angle α. So, it’s basically written as "tan α = a / b," where 'a' is the length of the side opposite and 'b' is the length of the side adjacent. This simple little formula, you know, packs a lot of punch when it comes to solving problems involving triangles. It’s a very direct way to connect angles to lengths, and it’s used a lot.

Is There More to the Tangent Story?

Interestingly, the word "tangent" has another meaning, one that isn't about geometry or triangles at all. It can also mean a sudden, unexpected shift in direction or topic. Think about a conversation that's going along smoothly, and then someone suddenly, you know, brings up something completely unrelated, and the whole discussion takes a sharp turn. That's taking a tangent. It’s an abrupt change of course, a departure from the main point. This meaning, actually, is quite common in everyday language.

A Sudden Turn - The Tangent SNL as a Shift

When someone says, "Oh, sorry, I went off on a tangent," they mean they, you know, veered away from the main subject. It’s like their thoughts or words suddenly, and without much warning, took a different path. This sense of the word "tangent" is, in fact, quite vivid. It paints a picture of something that was on one track suddenly moving to another, perhaps a bit unexpectedly. It’s a very human way to describe how our minds, or conversations, can sometimes operate, you know, with those little detours.

The way we use "tangent" in a sentence often points to this idea of a sudden change. For example, you might say, "The speaker went on a tangent about his cat, completely forgetting the topic of the meeting." This means the speaker, you know, made an abrupt change in what they were talking about. It’s a word that captures the feeling of something just, well, not sticking to the script. It’s a pretty common occurrence in daily life, and it’s interesting how a mathematical term can also describe something so, you know, human and unpredictable.

This idea of an abrupt change of course, or a sudden departure, is, you know, quite a powerful way to think about things. It suggests a moment where something that was following one path suddenly decides to follow another. It’s not necessarily a negative thing; sometimes these tangents lead to interesting discoveries or, well, funny moments. It's just a shift, a sudden movement away from what was expected. It’s a very dynamic concept, in a way, describing movement and change.

So, we have the geometric tangent, which is a line that just touches a curve, and then we have this other meaning, which is a sudden, unexpected shift. Both ideas, in a way, involve a kind of "touch" or "connection" that then leads to something else. One is about a precise mathematical relationship, and the other is about, you know, a less predictable, more conversational turn. It’s pretty neat how one word can hold these two rather different, yet subtly connected, meanings. It just goes to show how language can be, you know, quite rich.

Where Do We Even Use the Tangent?

Beyond the classroom, the tangent function, especially in its trigonometric form, finds a good number of uses. It's not just for, you know, doing homework problems. It helps people figure out unknown details in right-angled triangles when they already know some other bits of information about the triangle's legs. For example, if you know how long one side is and the angle, you can use the tangent to figure out how long another side must be. It's a very practical tool for measurement and design.

Figuring Things Out - The Tangent SNL in Action

Think about someone building a ramp or, you know, trying to measure the height of a tall building without actually climbing it. If you know the distance from the base of the building and the angle you have to look up to see the top, you can, in fact, use the tangent function to calculate the building's height. It's a way to find missing information in situations where you can't directly measure everything. This is, you know, pretty helpful for engineers, architects, and even people doing simple DIY projects. It's a very real-world application of what might seem like an abstract idea.

The tangent function is, therefore, quite useful for solving problems that involve triangles and angles. It’s one of the main tools in what’s called trigonometry. This field of study helps us, you know, understand how angles relate to distances, which is incredibly important in fields like surveying, astronomy, and even video game development. When you think about it, any time you need to work out distances or heights based on angles, the tangent is likely to be one of the things you reach for. It’s a rather versatile mathematical helper, you know.

It’s also fundamental to calculus, which is a higher level of mathematics that deals with rates of change and accumulation. The geometric tangent line, the one that just touches a curve, is, in fact, a core idea in calculus for figuring out the exact slope of a curve at any given point. This helps us, you know, understand how things are changing at an instant, whether it’s the speed of a car or the growth of a population. So, it’s not just about static shapes; it’s about understanding movement and transformation too.

So, from drawing a simple line that kisses a curve to calculating distances in a triangle, and even describing those unexpected turns in a conversation, the idea of a "tangent" is, you know, quite a versatile concept. It shows up in different ways, but each time, it’s about a particular kind of connection or a sudden shift. It’s a reminder that even seemingly complex mathematical ideas can have, well, very relatable meanings and uses in our everyday lives. It’s pretty interesting how it all connects, you know.

Tangent | Definition | Equation and Calculator - Cuemath

Details

Tangent Formula - What Are Tangent Formulas? Examples

Details

Tangent of a Circle - GCSE Maths - Steps, Examples & Worksheet

Details

Detail Author:

Name : Christiana Crooks
Username : lebsack.calista
Email : bergstrom.nat@gmail.com
Birthdate : 1980-02-19
Address : 981 Gusikowski Groves Lake Annetta, PA 49599-0337
Phone : +1 (903) 471-0249
Company : Dickinson, Brekke and Dickens
Job : Manufactured Building Installer
Bio : Eligendi qui qui atque rerum dolorem corrupti. Explicabo ab tempora ducimus magni necessitatibus ipsam modi. Totam et omnis ipsa consequatur consectetur. Sint quis est ut repellendus nesciunt.